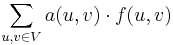Minimum-cost flow problem

The minimum-cost flow problem is finding the cheapest possible way of sending a certain amount of flow through a flow network.

1 Definition
2 Relation to other problems
3 Solutions
4 See also
5 References
6 External links

Definition

Given a flow network 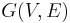$\,G(V,E)$ with source 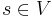$s \in V$ and sink 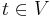$t \in V$ , where edge 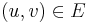$(u,v) \in E$ has capacity 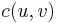$\,c(u,v)$ , flow 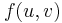$\,f(u,v)$ and cost 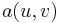$\,a(u,v)$ . The cost of sending this flow is 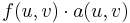$f(u,v) \cdot a(u,v)$ . You are required to send an amount of flow 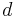$\,d$ from s to t.

The definition of the problem is to minimize the total cost of the flow:

$\sum_{u,v \in V} a(u,v) \cdot f(u,v)$

with the constraints

Capacity constraints:	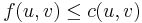$\,f(u,v) \le c(u,v)$
Skew symmetry:	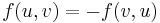$\,f(u,v) = - f(v,u)$
Flow conservation:	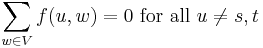$\,\sum_{w \in V} f(u,w) = 0\text{ for all }u \neq s, t$
Required flow:	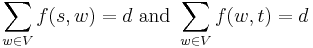$\,\sum_{w \in V} f(s,w) = d\text{ and }\sum_{w \in V} f(w,t) = d$

Relation to other problems

A variation of this problem is to find a flow which is maximum, but has the lowest cost among the maximums. This could be called a minimum-cost maximum-flow problem. This is useful for finding minimum cost maximum matchings.

With some solutions, finding the minimum cost maximum flow instead is straightforward. If not, you can do a binary search on $d$ .

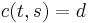A related problem is the minimum cost circulation problem, which can be used for solving minimum cost flow. You do this by setting the lower bound on all edges to zero, and then make an extra edge from the sink $t$ to the source $s$ , with capacity $c(t,s)=d$ and lower bound 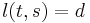$l(t,s)=d$ , forcing the total flow from $s$ to $t$ to also be $d$ .

The problem can be specialized into two other problems：

if the capacity constraint is removed, the problem is reduced to the shortest path problem,
if the costs are all set equal to zero, the problem is reduced to the maximum flow problem.

Solutions

The minimum cost flow problem can be solved by linear programming, since we optimize a linear function, and all constraints are linear.

Apart from that, many combinatorial algorithms exist, for a comprehensive survey, see ^[1]. Some of them are generalizations of maximum flow algorithms, others use entirely different approaches.

Well-known fundamental algorithms (they have many variations):

Cycle canceling: a general primal method.^[2]
Minimum mean cycle canceling: a simple strongly polynomial algorithm.^[3]
Successive shortest path and capacity scaling: dual methods, which can be viewed as the generalizations of the Ford–Fulkerson algorithm.^[4]
Cost scaling: a primal-dual approach, which can be viewed as the generalization of the push-relabel algorithm.^[5]
Network simplex: a specialized version of the linear programming simplex method.

References

^ Ravindra K. Ahuja, Thomas L. Magnanti, and James B. Orlin (1993). Network Flows: Theory, Algorithms, and Applications. Prentice-Hall, Inc.. ISBN 0-13-617549-X.
^ Morton Klein (1967). "A primal method for minimal cost flows with applications to the assignment and transportation problems". Management Science 14: 205–220.
^ Andrew V. Goldberg and Robert E. Tarjan (1989). "Finding minimum-cost circulations by canceling negative cycles". Journal of the ACM 36 (4): 873–886.
^ Jack Edmonds and Richard M. Karp (1972). "Theoretical improvements in algorithmic efficiency for network flow problems". Journal of the ACM 19 (2): 248–264.
^ Andrew V. Goldberg and Robert E. Tarjan (1990). "Finding minimum-cost circulations by successive approximation". Math. Oper. Res. 15 (3): 430–466.

External links

LEMON C++ library with several maximum flow and minimum cost circulation algorithms